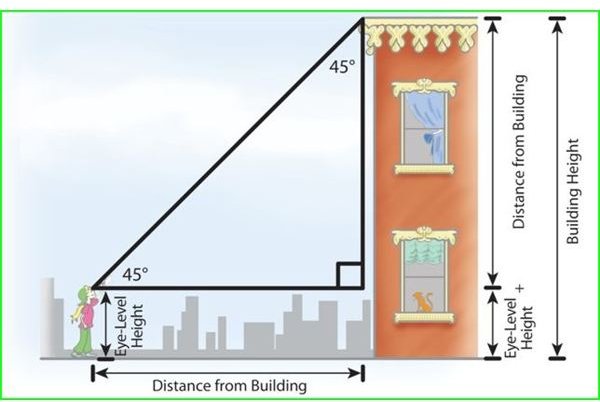
Use the position function st 49t² v0 t s0 for free falling objects. How high is the building if the. The height of a falling object can be approximated assuming no air resistance by ht 16t2 h0where h0 is the initial height of the objectwe are given h56 0 and are asked to find h0. To estimate the height of a building a stone is dropped from the top of the building into a pool of water at ground level. 0 16562 h0 16562 h0 50176 h0the height of the building is about 500 ft. Use the position function for free falling objects given below.

H is the height of the fall. How high is the building if the splash is seen 92 seconds after the weight is dropped. T is the duration of the fall. Round your answer to one decimal place st 49t 2 v 0 t s 0. Round your answer to one decimal place s 49t2 vot so. This is a simplification of the general formula of distance traveled under constant acceleration.

What is the height of the building. The splash is seen 66 seconds after the stone is dropped. D x vt ½at². To estimate the height of a building a stone is dropped from the top of the building into a pool of water at ground level. The formula for height based on time of fall is. G is the acceleration due to gravity.

Answer 1 of 1. The splash is seen 56 seconds after the stone is dropped. To estimate the height of a building a stone is dropped from the top of the building into a pool of water at ground level. To estimate the height of a building a weight is dropped from the top of the building into a pool at ground level. What is the height of the building. Use the position function below for free falling objects.

The position function is s t 49t² to estimate the height of a building a stone is dropped from the top of the building into a pool of water at ground level. How high is the building if the splash is seen 63 seconds after the stone is dropped.

Gallery of To Estimate The Height Of A Building A Weight Is Dropped From The Top