What Type Of Correlation Exists Between Height And Weight

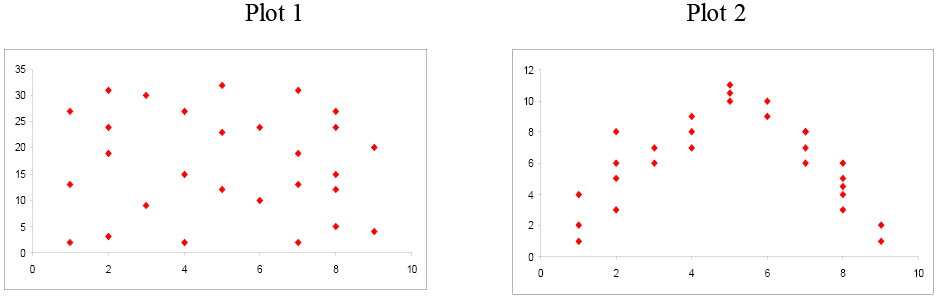
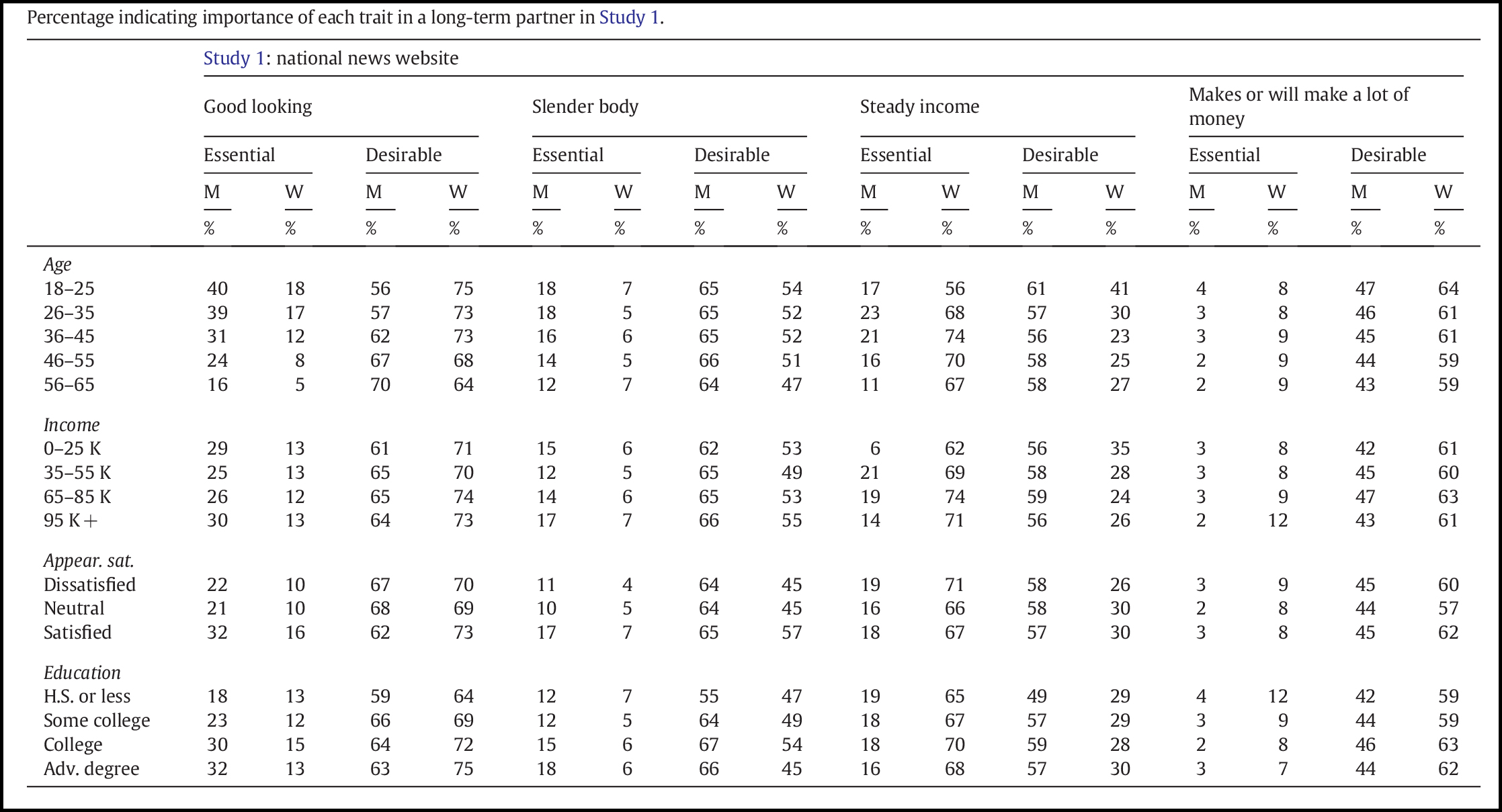
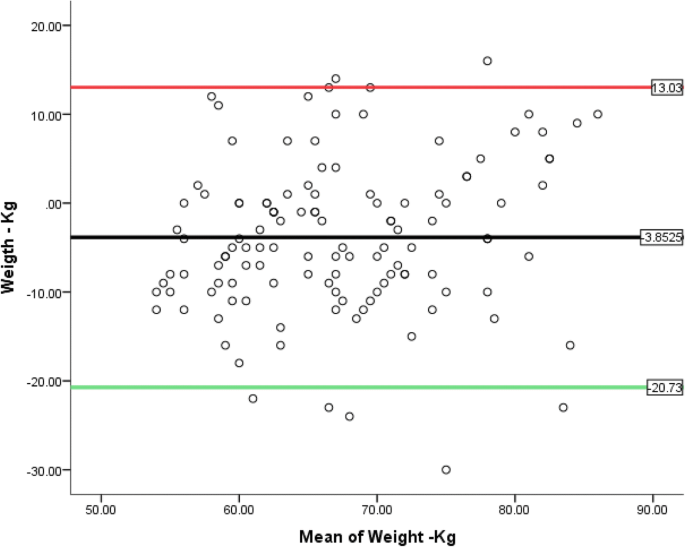
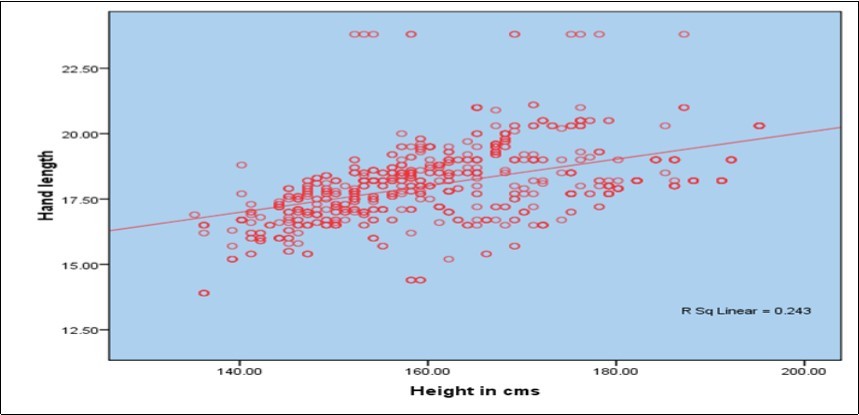
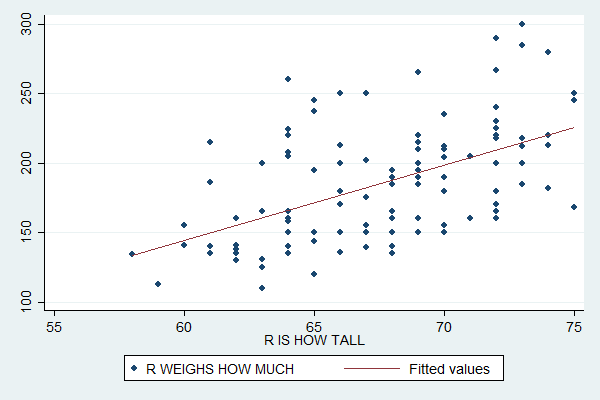
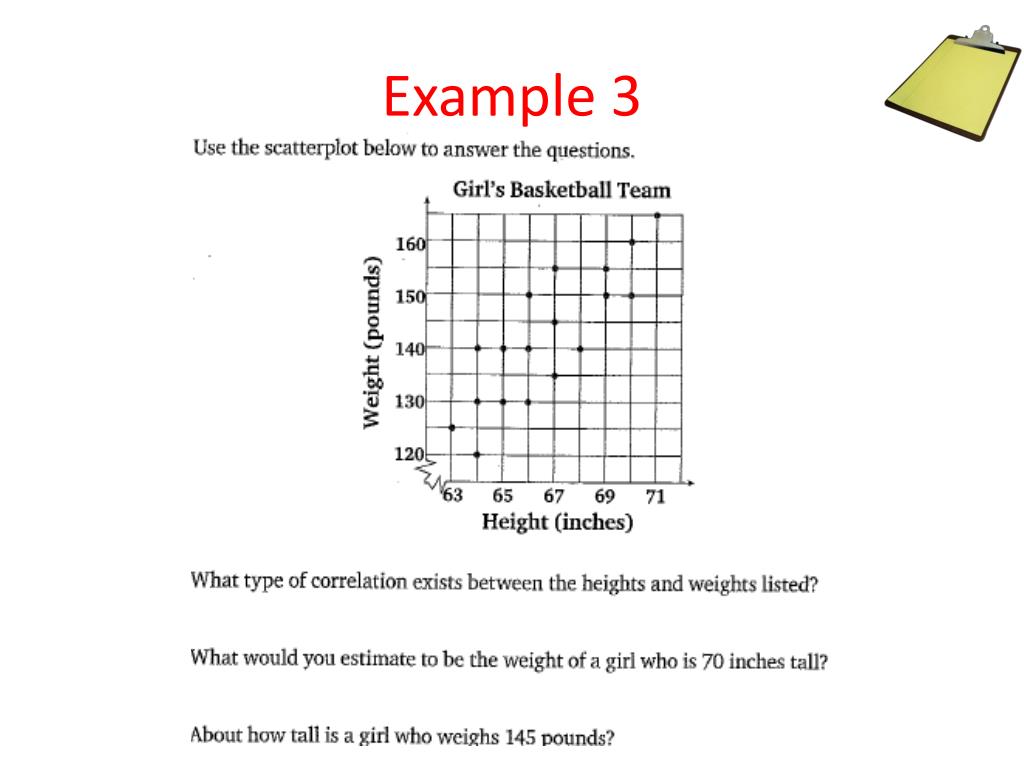
Theres a strong correlation between height and weight. This correlation is statistically significant p00001. A correlation also measures the strength of the relationship between x and y. Taller people tend to be heavier. The value of r for this data set is 076. People of the same height vary in weight and you can easily think of two people you know where the shorter one is heavier than the taller one.

As we expect this is much higher than a value of zero thus indicating a correlation between the variables. Take a look at the correlation between the height and weight data 0694. The students want to know if a similar relationship exists between. In the example data set above the scatterplot and regression line lead us to believe there is a correlation between height and weight. Its not a very strong relationship but it accurately represents our data. A correlation will have a value between 1 and 1.

In other words a 10 increase in height is tied to a 31 increase in weight. Nonetheless the average weight of people 55 is less than the average weight of people 56 and their average weight is less than that of people 57 etc. Linear eg height and weight non linear eg age and height 3 the degree of the relationship. An accurate representation is the best case scenario for using a statistic to describe an entire dataset. That is there is evidence of a relationship between weight and height in the population. An example of positive correlation would be height and weight.

The correlation between weight and height is r0717301. A negative correlationis a relationship between two variables in which an increase in one variable is associated with a decrease in the other. Type of hypothesis test. Correlation can tell you just how much of the variation in peoples weights is related to their heights. The correlation coefficient should accurately reflect the strength of the relationship. A correlation of 0 means that there is no relationship.

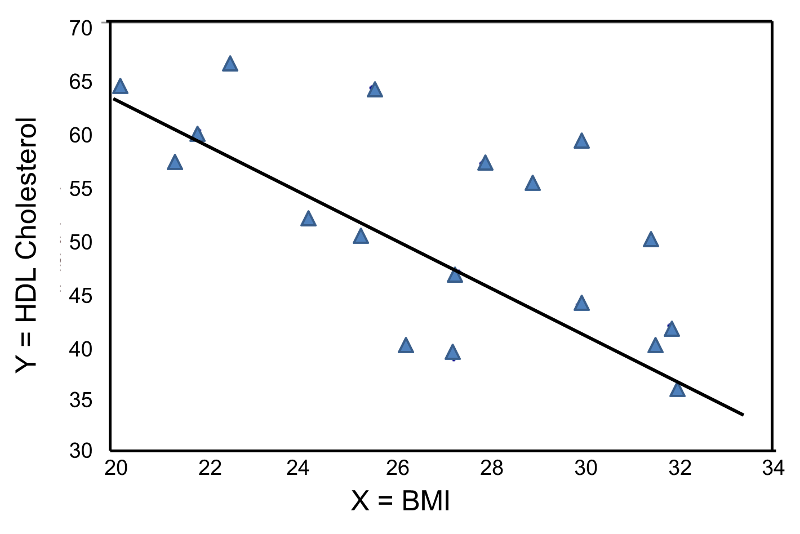
A value of 1 indicates a perfect correlation between the variables. It is one of the best means for evaluating the strength of a relationship. Many studies have found this relationship. An example of negative correlation would be height above sea level and temperature. In general weight increases as the cube of the increase in height. For example we know that the correlation between height and weight is approximately r70 if we square this number to find the coefficient of determination r squared49 thus 49 percent of ones weight is directly accounted for ones height and vice versa.