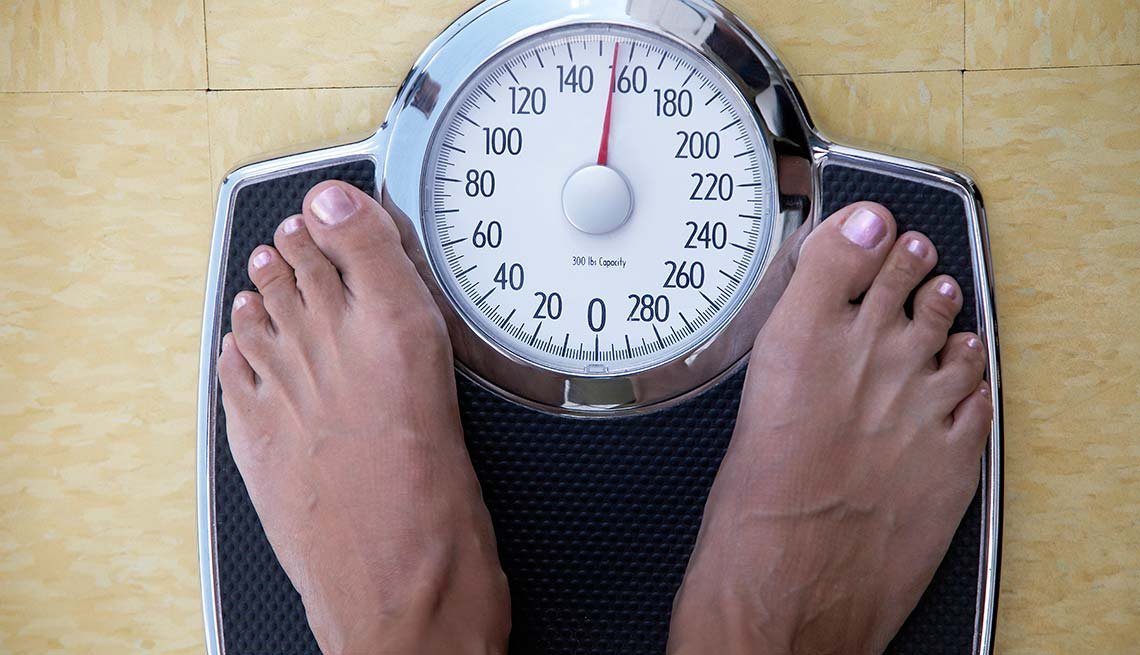
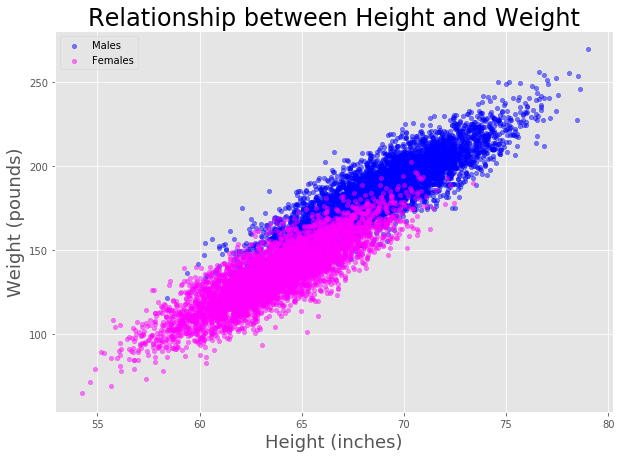
Height in centimeters minus 110. Below are some average values for different age groups in graph and table form. Thus if a correlation of 08 is observed between two variables say height and weight for example then a linear regression model attempting to explain eithervariable. Historically there have been two main approaches to systematizing the relationship between mass and force. Height in centimeters minus 100. Mass force weight.
For people under 40 the formula is as follows. The dubois and dubois formula 2 bsa m2 020247 x height m0725 x weight kg0425 a variation of dubois and dubois 15 that gives virtually identical results is. The result is in squared meters which easily be converted to square feet inches or yards as needed. Relevance and uses of regression formula. The square of the correlation coefficient r² is a useful value in linear regression. It appears that there is a significant very less relationship between height and weight as the slope is very low.
Bsa m2 0007184 x height cm0725 x weight kg0425. The key to keeping them straight is to remember newtons law the 2nd law of motion. Lets now input the values in the formula to arrive at the figure. The units for working with mass and force tend to be confusing for many students. For people above 40. It takes into account the correlation between a persons height weight body type and age.
020247 x height m0725 x mass kg0425 where height is in meters and mass is in kg. Hence the regression line y 6863 007 x.







/GettyImages-848079198-5af08caea18d9e0037582da7.jpg)