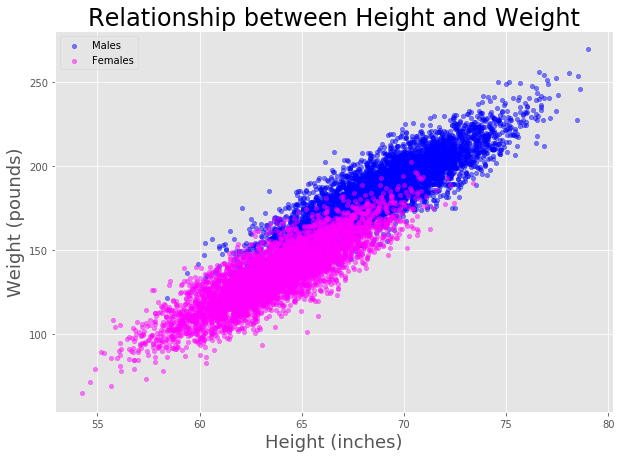
For example we know that the correlation between height and weight is approximately r70 if we square this number to find the coefficient of determination r squared49 thus 49 percent of ones weight is directly accounted for ones height and vice versa. A value of 0 indicates no relationship between the variables. Theres a strong correlation between height and weight. The following dataset shows the height and weight of 12 individuals. Make a scatterplot of height vs weight to visualize the correlation. The value of r for this data set is 076.

Find the mean standard deviation and 95 confidence interval for both variables. In the example data set above the scatterplot and regression line lead us to believe there is a correlation between height and weight. Suppose you converted the data to feet. The correlation coefficient should accurately reflect the strength of the relationship. Back to statistics main page. The test statistic t 836 12 2 1 836 2 4804.

A value of 1 indicates a perfect correlation between the variables. The scatterplot below shows the value of these two variables. So for example you could use this test to find out whether peoples height and weight are correlated they will be the taller people are the heavier theyre likely to be. Its not a very strong relationship but it accurately represents our data. The pearson correlation coefficient is used to measure the strength of a linear association between two variables where the value r 1 means a perfect positive correlation and the value r 1 means a perfect negataive correlation. Pearson correlation coefficient calculator.

In general weight increases as the cube of the increase in height. As we expect this is much higher than. Take a look at the correlation between the height and weight data 0694. However there is only one correct answer. In other words a 10 increase in height is tied to a 31 increase in weight. In the first question height is measured in inches.

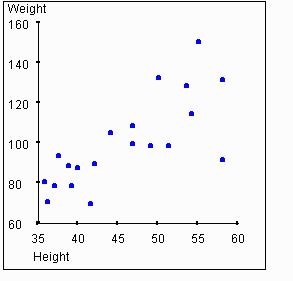
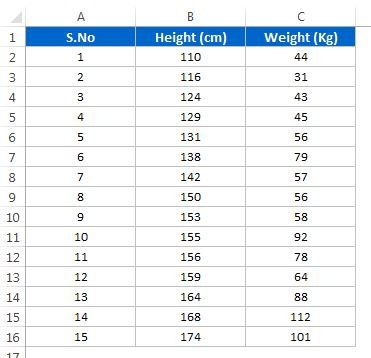
Calculate the correlation coefficient of height and weight. The pearson correlation coefficient for these two variables is r 0836.

Gallery of Correlation Coefficient Between Height And Weight